Mattia Nardin
Ph.D. degree on 18/04/2023
A 4-node nite element for a generic quadrilateral plane domain is developed to compute Strain Gradient theory as Mindlin proposed in 1968 [1, 2].
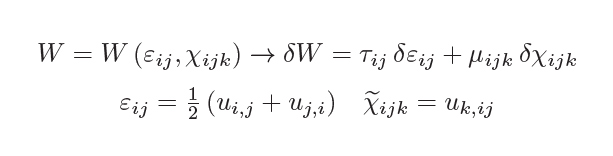
Starting from elements developed for Kirchhoff-Love plate theory (Adini-Clough-Melosh and Bogner-Fox-Schmit [3]), three types of quadrilateral Hermitian element with respectively 6, 8 and 12 degrees of freedom (DoFs) for nodes, with sub-parametric geometric transformation, are implemented in MatLAB (Fig.1).
The DoFs associated with the vertices correspond to the value of displacement field and its first/second/mixed derivatives at those points. The correspondence between DoFs and field derivatives values ensures a high order in the interpolation of the in-plane displacement, with a polynomium of degree 6 when the finite element is described through twelve DoFs. The virtual work principle is exploited to derive the weak form of the equilibrium equations and complex geometries are interpolated by adopting different shape functions determining sub-parametric elements. The performances and the accuracy of the quadrilateral elements are finally evaluated through comparison with available analytical solutions in plane strain elasticity. Numerical results available in literature are compared with those obtained exploiting the proposed Finite Elements code. The majority of examples use a isotropic constitutive model proposed by Aifantis [4] that has in addition to classical Lamè constants (λ and μ) only one parameter l called characteristic length.
References
[1] R.D. Mindlin. Micro-structure in linear elasticity. 1964.
[2] R.D. Mindlin and N.N. Eshel. On first strain-gradient theories in linear elasticity. 1968.
[3] R.L. Fox F.K. Bogner and L.A. Schmit. The generation of interelement compatible stiffness and mass matrices by the use of interpolation formulas. 1992.
[4] E. C. Aifantis. On the role of gradients in the localization of deformation and fracture. 1992.