Güner Tugberk, Ph.D. Candidate 36th cycle, University of Trento, DICAM
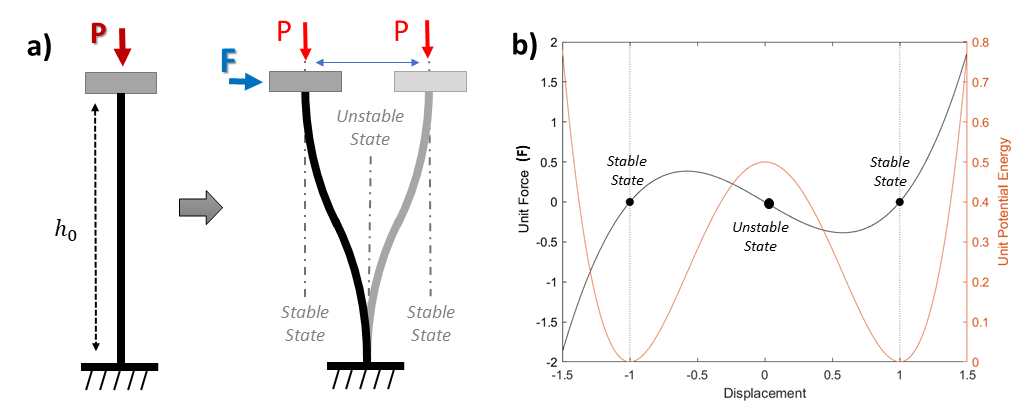
In recent years, bistability has drawn great attention owing to its intricate and valuable dynamics. A bistable structure that has two local minima of potential energy can be designed using a buckled column as shown in Fig. 1. Recent years have seen various investigations on the topic of nonlinear periodic structures utilizing bistability to reveal their charming wave dynamics properties. As opposed to linear counterparts, the dynamics are sensitive to the wave amplitude, and various phenomena can be observed such as amplitude-dependent dispersion, nonreciprocity, chaos, solitons, and many others. As a novel approach, a resonator is considered to be attached to the bistable unit cell. In a linear system, this leads to internal resonances centered at the resonant frequency of the resonator which creates a bandgap. Concerning the properties of a bistable system, the aim is to achieve the advantage of harmonic diffusion to diffuse internal resonances and provide a wider bandgap(s).
Fig. 1
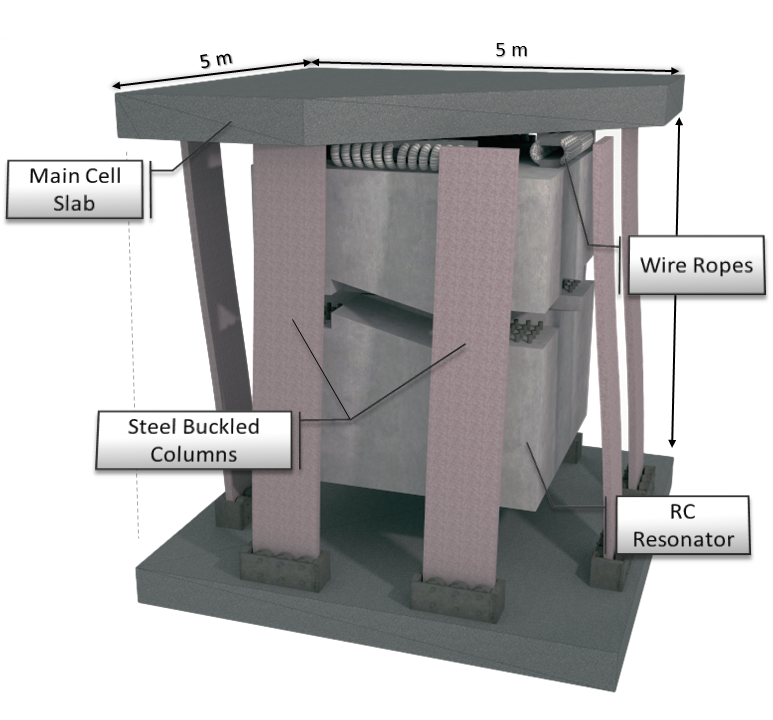
Stated bistable mass-in-mass periodic systems can be used to create structural metamaterial which can exhibit subwavelength band-gaps. Shortly the aim is to attenuate low‐frequency seismic waves by engaging efficient and cost-friendly dissipative acoustic metamaterials as seismic dissipation layers and prevent seismic waves to reach the superstructure in band-gap regions. The proposed metafoundation, so-called bistable metafoundation (BM), simply comprises multiple bistable mass-in-mass cells as a foundation where the main cell contains prebuckled steel columns and a rigid slab. The details of the unit cell of the BM can be observed in Fig. 2.
Fig. 2
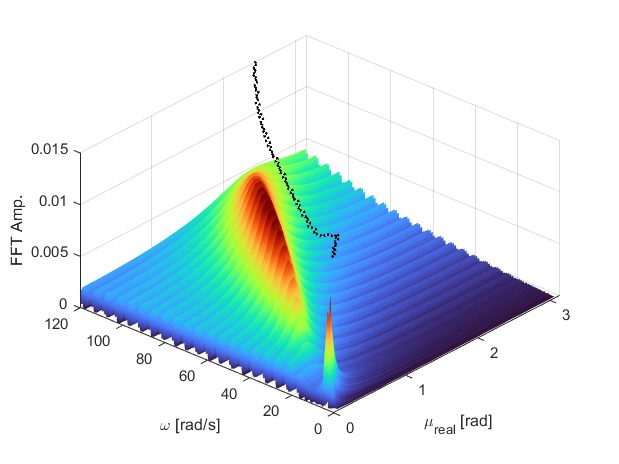
The proposed BM is considered to protect a superstructure composed of a slender anchored storage tank and consequently two BMs, with single and double layers, are designed, optimized, and analyzed. Considering the designed BMs, structural responses are compared by means of energy. To understand the underlying dynamics, BM unit cell is numerically and analytically investigated in a single cell and periodic chain formations. Followingly, frequency response, chaotic response probabilities, amplitude-dependent dispersion (Fig. 3), and wave propagation characteristics are revealed using computational tools such as FFT and Lyapunov exponent.
Fig. 3